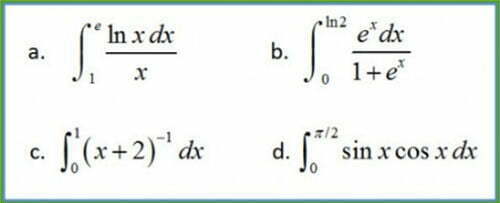Now that all my Calculus II students know about Wolfram Alpha (I showed them), I have to make sure that the assignments I ask them to turn in can’t just be “walphaed” with no thought. In Calc II, our topics list includes a lot of “techniques-oriented” topics (integration by partial fractions, integration by parts, etc.) and because of the need to keep this course transferable to 4-year schools, I can’t really get around this. So now I’m in the position of having to reconcile the use of technology that easily evaluates the integrals with making sure that students actually understand the techniques of integration. There are two ways I’m tackling this:
1. CCC (Concept Compare Contrast) Problems: I’m writing problems that focus on understanding the mathematical process and the compare/contrast nature of math problems. While Wolfram Alpha can evaluate the integrals for them, the questions I’ve asked require (I hope) a deeper level of understanding about what happens when the techniques are used. Here’s an example from my recent problem set:
There are two pairs of problems below that are exactly the same. You won’t see why until you do the integration, showing all the steps. Find the pairs and then explain how the matched integrals are fundamentally the same.
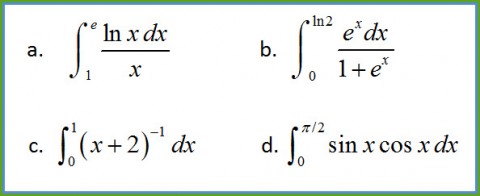
2. Inquiry Based Learning: One appropriate use for any CAS (computer algebra system) is to use it as a way for students to explore problem types that they have not learned about yet. Here’s a definition of IBL, in case you’re not familiar with the terminology:
Designing and using activities where students learn new concepts by actively doing and reflecting on what they have done. The guiding principle is that instructors try not to talk in depth about a concept until students have had an opportunity to think about it first (Hastings, 2006).
It is relatively easy to use IBL in the really low levels of math (K-6) where there is not as much abstraction of concepts. However, with the introduction of variables, rules, theorems, and definitions that come later in math, the use of IBL requires either that the instructor act as the inquiry tool or the use of CAS.
Back to the point (how to use Wolfram Alpha to do this): I could have just taught the integral techniques straight up … here’s the technique, now apply it … repeat. But learning the technique is not anywhere near as important (at least, in my mind) as learning to decide when to use a technique, i.e. what makes one integral different from another?
This semester, I’m doing it backwards. In the problem set before we look at specific techniques of integration, the students will use Wolfram Alpha to evaluate twenty integrals. Then they will look for patterns in the answers and the problems, and try, on their own, to make sense of what kinds of problems solicit different answers. After they understand what characteristics make one integral fundamentally different (in technique of integration) from another, then we’ll look at how each technique works. Below, you see a few examples of the integrals the students will explore.

For years, we’ve had CAS tools like Derive, Mathematica, Sage, Maple, etc. However, the use of these programs traditionally required so much coding minutia that the IBL often got lost in the coding. How do I know? Because this was my experience as a student. I had instructors that tried to teach me this way. All I remember is how painful the coding was. I followed the directions in the labs, I typed what I was supposed to type, and I answered the questions that were put forth to me. But in the end, I never sat down at a computer and generated my own inquiries. The details of using the programs were so painful that I just didn’t have any desire to use them after the class.
Here’s the sum total of the directions that were necessary for me to teach students how to evaluate integrals in Wolfram Alpha:
For example, here’s how to do the first one: http://www.wolframalpha.com/input/?i=integrate+10/(x^2-16)

I think Wolfram Alpha is a game-changing CAS (and no, I’m not being paid by someone to say this). For better or for worse, my students are now using W|A on their own, without any prompting from me. Their evidence of usage is showing up in emails, in discussion board questions, and in questions they ask in the classroom. Maybe my class is unusual because I’ve given them the first push… but it’s just a matter of time before W|A is discovered by your students too.