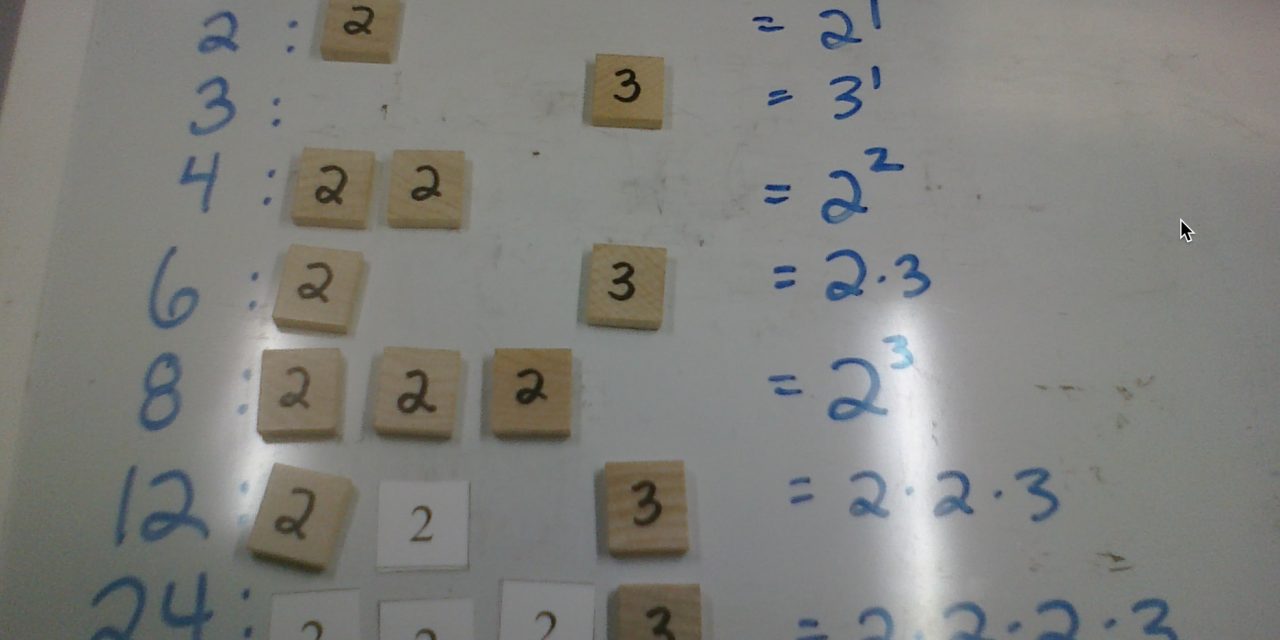
For those of you who are curious what we were actually doing in class in yesterday’s post (Record with a Document Camera and a Flip), we were “fingerprinting” the factors of composite numbers with their prime compositions. The wooden “prime number tiles” are created using the backs of Scrabble tiles and the white tiles you see on the board are the student version of the prime number tiles (each of them cut out a sheet of their own prime number tile manipulatives at the beginning of class). Just for the record, I would like to confess to destroying more than 5 Scrabble games in the last 6 months.

I tell students that the prime numbers are like the building blocks of the whole numbers, in the same way that the nucleotide bases (adenine, guanine, cytosine, and thymine) are the building blocks of DNA. It was ironic, then, that at the end of our prime factorization fingerprinting, the board looked (to me) the way an agarose gel electrophoresis looks.
You can also use the prime number tiles to line up the prime factorizations of two numbers (leaving spaces when the prime is not in both numbers) and read the GCF as the intersection of the two lines of tiles and the LCM as the union of the two lines of tiles.


I’ve tried explaining these concepts in writing before (circling common factors and using colors or highlighting to show the steps), but the ability to easily rearrange the prime numbers after they’ve been found makes all the difference. Students find the prime factorization using a factor tree or short division, then place out all the tiles for each number. At this point, they can rearrange each row into least-to-greatest order. Then line up the primes, bumping the whole row when there is no overlap in primes between the composite numbers.
We also were able to look at more interesting problems now that students could “see” the inner workings of the factorizations better. For example, find a pair of numbers with a GCF of 42 and an LCM of 4620 (you may not use the “trivial” answer of 42 and 4620). By constructing a “board” of prime number tiles, starting with the factorization of the GCF and the LCM, students begin to see which primes have to be in the two numbers and which can only be in one of the two numbers. Note that there will be more than one answer here … which is another interesting discussion to have!
I’ve never seen “prime number tiles” in any math manipulative kit … they were just something I created last semester. I think this method of using Prime Number Tiles would also be helpful with explaining how to find the GCF in the factoring unit of algebra, and with explaining how to find the LCD in fractions.