As I watch the proliferation of digital learning platforms, particularly in STEM education (where there are lots of objective-type problems), I am excited by the increased focus on learning and adaptivity but also a little uneasy. For the most part the motivations to “go digital” are pure – increase access to courses that students need, provide help that is more tailored to each student, give immediate feedback, provide more practice if the student wants it, and let students move at their own pace.
My worry is that math and science students aren’t getting anything but highly-structured problems. Every problem that a computer delivers is one where there is a carefully constructed set of constraints on the problem and a highly uniform (and thus gradable) answer.
But the problems of the real world aren’t carefully constrained and the problem solutions aren’t highly uniform. If we only teach students to solve the “lives in an orderly box” kind of problems, what are we preparing them for? Are we creating experiences that lead to curiosity in STEM subjects? Do students even see subjects like math as highly connected networks of concepts or just as discrete concepts to be learned one-at-a-time inside a digital system?
What is a Problem Elaboration?
This semester I’ve fallen back on a very old assessment technique I developed about 15 years ago that I call a “Problem Elaboration.” Students have to turn in a two problems per topic/section where they complete the problem (the old-fashioned way on paper) and then do some kind of mathematical elaboration on the problem. In other words, they have to do something that wasn’t asked for. They have to think in the space around the problem and consider:
- What else could I find?
- What other mathematical things could I do with this?
- How does this connect to other things we’ve learned?
- How could I check this to make sure it’s right?
It’s fascinating to watch the initial struggle of many of the students with the sudden freedom of elaborations. Students fall into three categories in the beginning of the term, but every student that makes an honest effort moves up this ladder to increasingly creative and complex elaborations over time.
Trepidatious: How am I supposed to find something that I’m not asked to find? I don’t even know how to begin! This is crazy! Your job is to support these students with examples, suggestions, and a “you can do it” attitude. These students will eventually try, and when they do, encourage them!
Compliant: If there is some way to check the problem, I’ll do that. If I wasn’t asked to graph the problem I’ll do that. These are the not the most creative elaborations. But it is an exploration that contributes to mathematical maturity. This tends to end up being what students do when they are short on time.

Elaboration 1: Notice the actual problem is highlighted in a lighter color. The elaboration is to check the answer. It’s not particularly glamorous, but the student knows how to check the answer, she knows it’s right, and that’s pretty awesome.
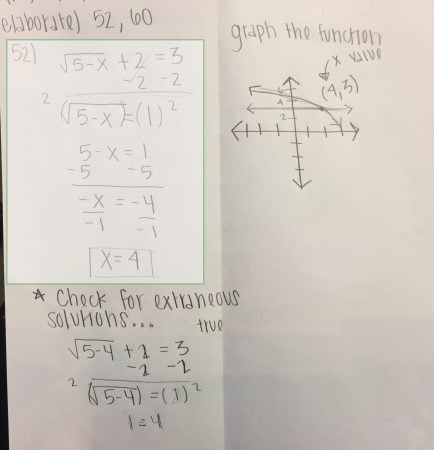
Elaboration 2: This also has the standard “check your answer” type of elaboration, but it goes one step further. This student shows me that she knows how to GRAPH both sides of the equation and verify that she has the right solution!
Curious: What happens to this graph if I change this number or this sign? I did “X” and was expecting “Y”. Why didn’t that work? How does this connect to what we did yesterday? How would I find this thing I don’t know how to find?

Elaboration 3: Now we see an elaboration that really begins to explore the “what happens if” space. What happens if this is a 5th root instead of a square root? What happens if there is a number multiplied by the square root in the original equation?

Elaboration 4: This students starts by checking the answer, noting where they made a mistake the first time, and redoing the check. Then the student explores whether they can square individual terms in the equation instead of isolating the square root first and get the same answer. See the question the student is left with? “Not sure if that means something or not.” That’s the opener to a conversation in pen pal form about the right way that squaring both sides actually works.
As I grade these assignments, I find that what I’m really doing is opening up a conversation with the student. The elaborations aren’t always right, and often the students are asking questions in the elaborations. This is our chance to explore the math together in a back-and-forth letter to each other, assignment after assignment. Over the course of a semester, I watch many students develop mathematical maturity, mathematical confidence, and ownership of the math they have learned.
Logistics
I assign 2 problems to turn in with elaboration per topic, using a particular grading rubric for these problems, based on 5 points:
- 1 point for rephrasing or rewriting the problem (students end up solving a slightly miscopied problem, or don’t catch all the parts of the problem)
- 2 points for showing all appropriate work to solve the problem
- 1 point for actually finding the correct answer
- 1 point for the elaboration
I also award a bonus point for really great and thoughtful elaborations (at discretion of instructor). Typically students earn between 0 and 5 bonus points per unit depending on their effort and thoughtfulness.
If a student makes an honest and thoughtful attempt at an elaboration, they will get the point even if their elaboration ends up being wrong or using incorrect terminology. The point is that the student explores and tries. My role is to correct improper terminology and to help when their reasoning wanders into an area where it no longer holds.
At the beginning of the semester, I do provide some idea of what an elaboration might be. A single elaboration might be any one of the following, but this is not an all inclusive list of what could be done.
- Show a different way to solve the problem.
- Show how to check the answer.
- Solve for something extra in the problem.
- Relate the concepts in this problem to something else we’ve studied.
- Relate the concept in the problem to a graph (if there wasn’t a graph required in the problem).
- Hypothesize on how a change to the problem might change the answer, and then try it.
- If it relates to this problem, investigate something we did in class that you found difficult to understand or remember.
Why the unease?
Online learning and learning through digital platforms is highly structured and scripted. Students learn exactly what they are scripted to learn. They only “explore” in the sense that we sometimes allow them to choose the next highly-scripted chunk of learning they engage with.
How do we build digital learning spaces where something like elaborations and this personal conversation between myself and the student about the mathematics can also be encouraged as a part of learning?
And if we don’t encourage our most engaged and curious students to go deeper, to question more, and to make more connections, what’s going to happen to our STEM pipelines?



